引言

粒子群优化（Particle Swarm Optimization, PSO）算法是一种基于群体智能的全局优化算法，由Kennedy和Eberhart在1995年提出。该算法模拟了鸟群觅食的行为，通过不断更新粒子的速度和位置来寻找最优解。PSO算法因其简单易实现、全局搜索能力强和适合并行处理等特性，在多个领域得到了广泛应用。本实验旨在通过具体案例，验证PSO算法在解决优化问题中的有效性。

算法描述

PSO算法的基本思想是通过模拟群体中的粒子（即解决方案候选）在搜索空间中的运动，不断调整位置和速度，从而找到最优解。具体步骤如下：

初始化：随机生成一组粒子，每个粒子代表一个可能的解决方案，并为其分配初始速度和位置。

计算适应度值：根据目标函数计算每个粒子的适应度值，通常适应度值越小表示解决方案越优。

更新个人最佳位置：如果当前粒子的适应度值优于其历史最佳适应度，则更新该粒子的个人最佳位置。

更新全局最佳位置：比较所有粒子的个人最佳位置，选取适应度值最小的作为全局最佳位置。

更新速度和位置：根据公式更新每个粒子的速度和位置，速度更新公式如下：

vij​(t+1)=w⋅vij​(t)+c1​r1​(pBestij​−xij​(t))+c2​r2​(gBest−xij​(t))

其中，vij​(t)是粒子i在维度j上的速度，xij​(t)是粒子i在维度j上的位置，w是惯性权重，c1​和c2​是学习因子，r1​和r2​是随机数。

重复步骤2-5：直到满足停止条件（如达到最大迭代次数、达到预定的精度等）。

实验设置

本实验实现PSO算法，具体设置如下：

粒子数量：20

最大迭代次数：100

惯性权重：1

学习因子：c1=

搜索空间范围：[-10, 10]

目标函数：rastrigin测试函数，Ackley测试函数，Sphere测试函数，beale测试函数，Booth测试函数，Bukin测试函数，Three-hump camel测试函数，Hölder table测试函数

实验结果

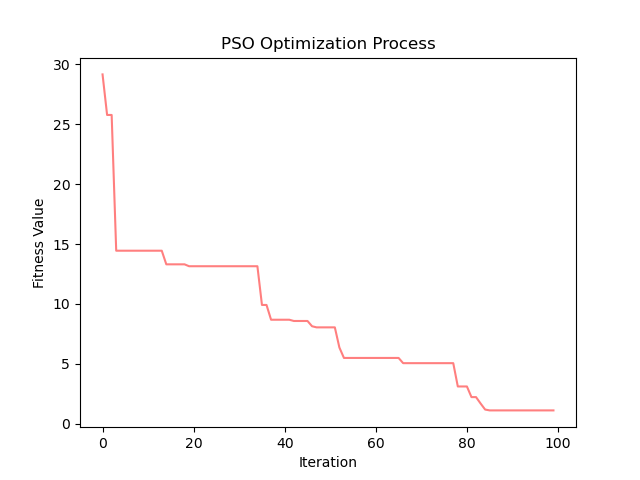
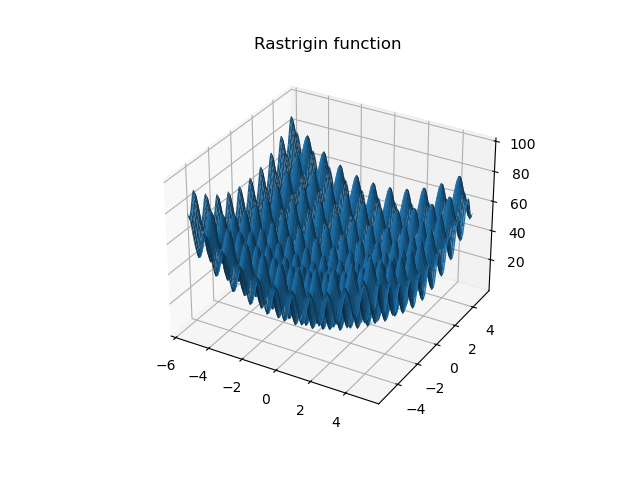
Rastrigin

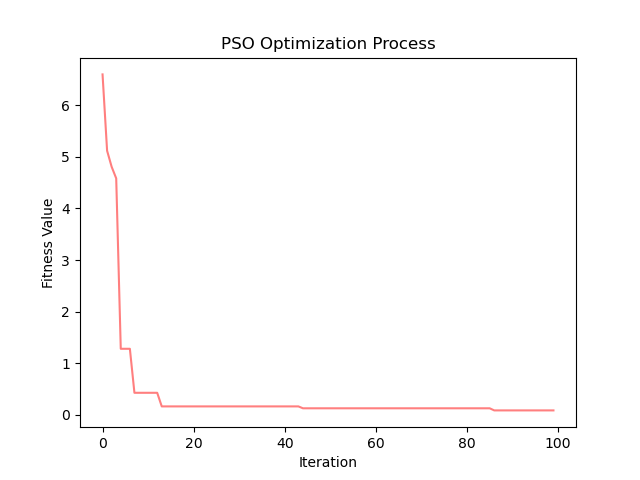
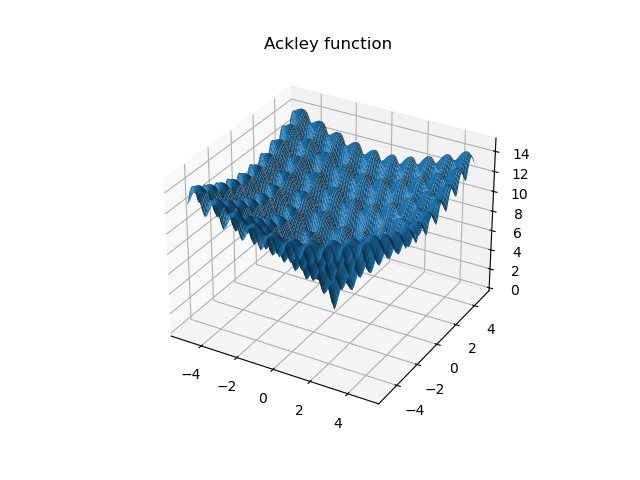
Ackley

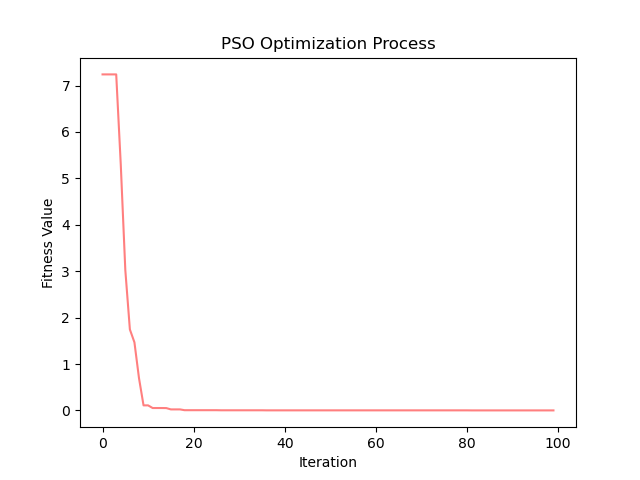
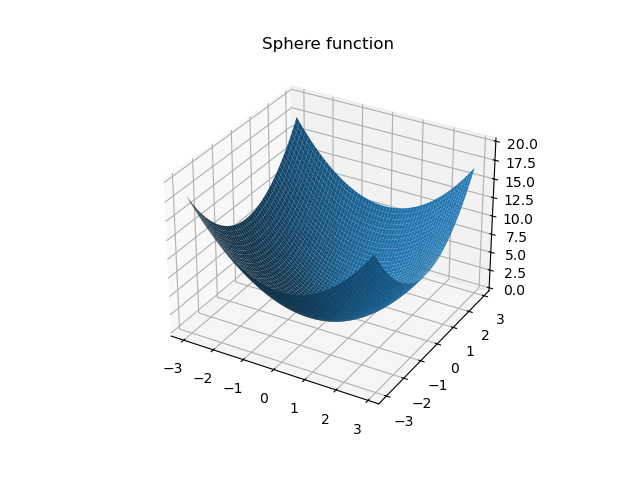
Sphere

`

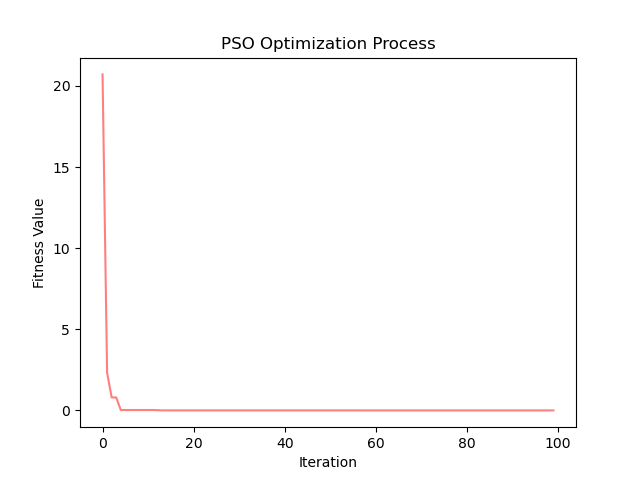
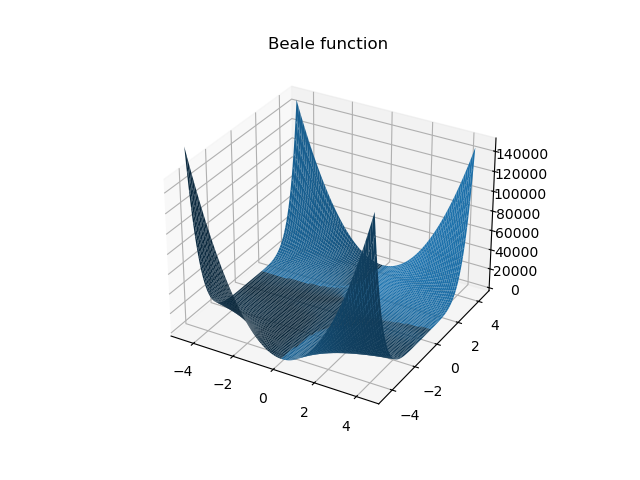
Beale

Booth

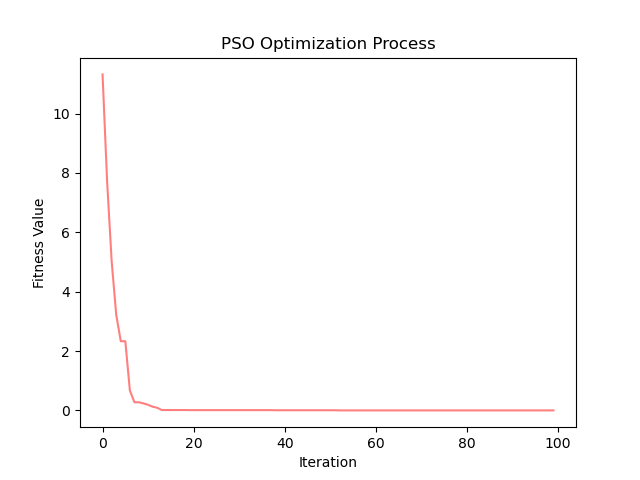
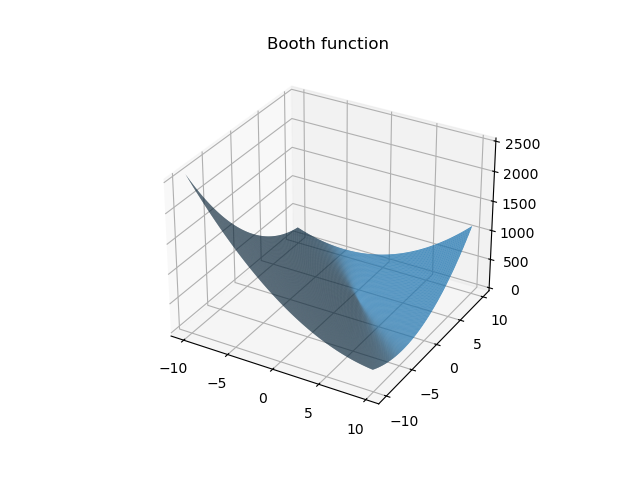
Bukin

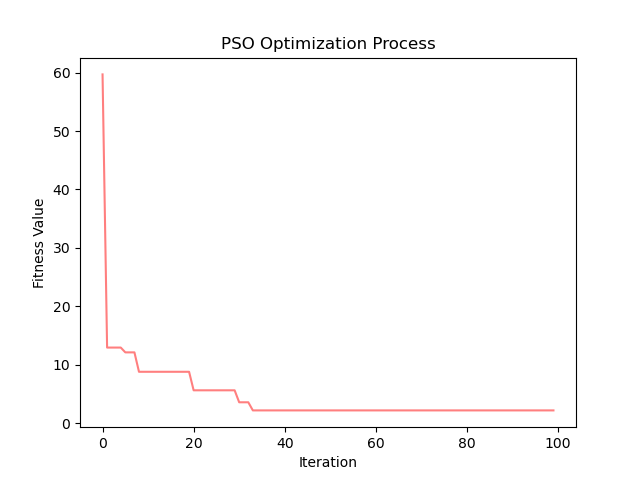
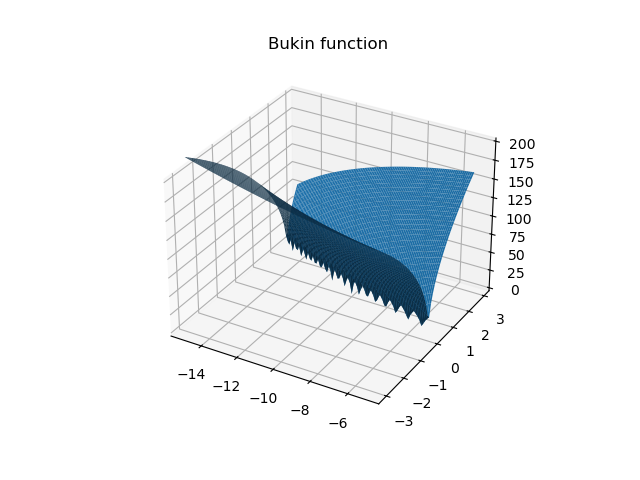
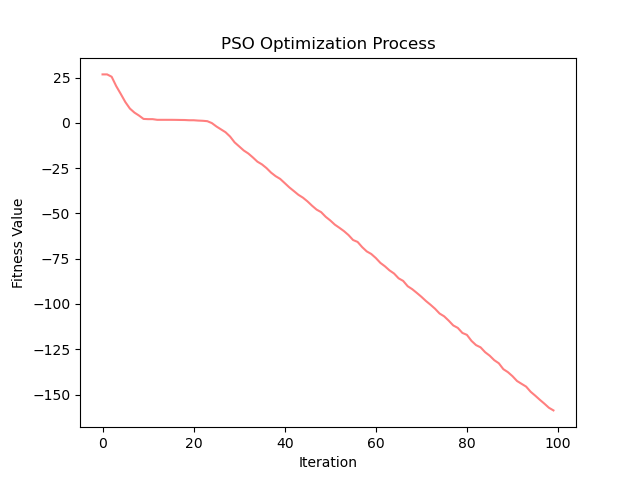
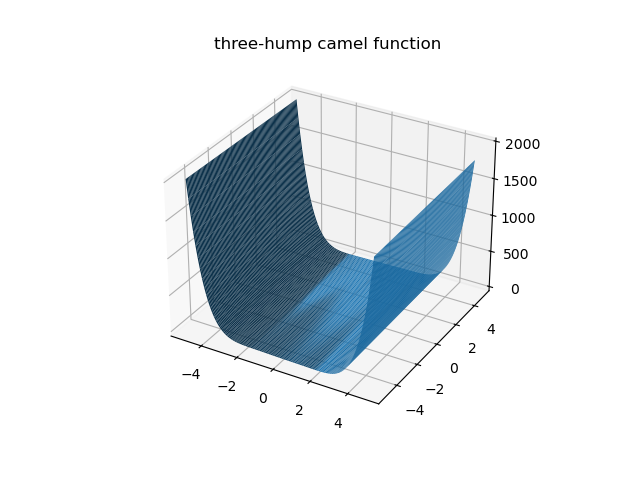
Three-hump camel

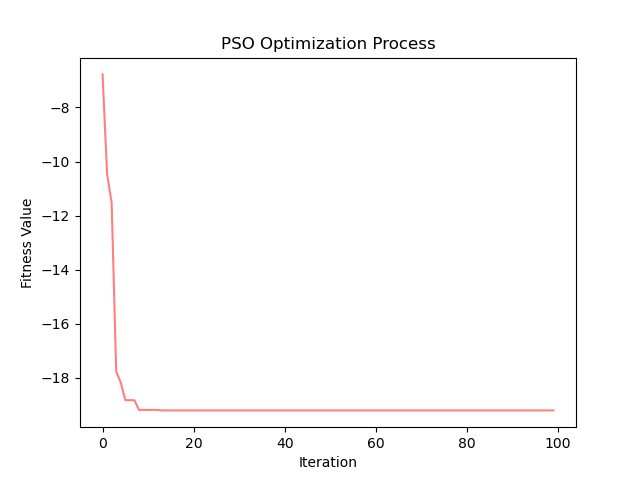
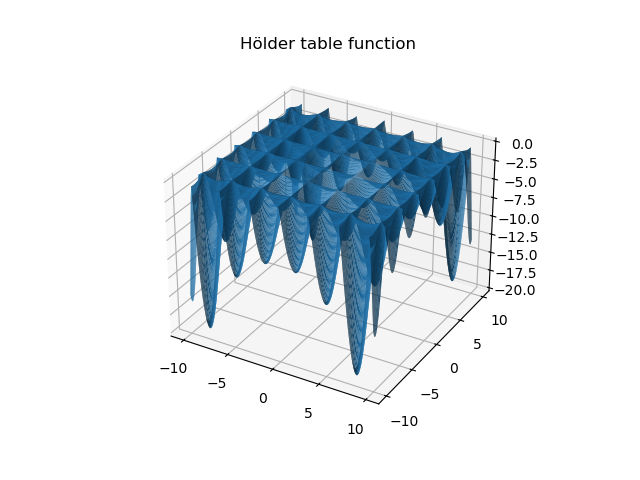
Hölder table

结论

本实验通过实现粒子群优化（PSO）算法，并对其在多种测试函数上的性能进行了验证。实验结果表明，PSO算法在解决全局优化问题方面表现出色，能够有效地找到这些测试函数的最优解或接近最优解。

首先，从实验结果来看，PSO算法在Ackley、Sphere、beale、Booth、Three-hump camel和Hölder table等测试函数上均取得了较低的最优解值，这表明算法在这些函数上具有较强的搜索能力和精度。尤其是在Sphere测试函数上，算法找到的最优解值非常接近理论上的全局最小值，这进一步证明了PSO算法在解决简单单峰函数问题上的高效性。

其次，对于具有多个局部最优解的复杂函数，如Bukin和rastrigin测试函数，PSO算法也能够成功地跳出局部最优，找到较好的全局最优解。尽管在这些函数上的最优解值相对较高，但考虑到这些函数的复杂性和多峰性，算法的表现仍然令人满意。

此外，从求解时间来看，PSO算法在所有这些测试函数上的运行时间都非常短，这表明算法具有较高的计算效率和实用性。这对于实际应用中需要快速找到解决方案的优化问题具有重要意义。

综上所述，本实验通过具体案例验证了PSO算法在解决全局优化问题中的有效性。实验结果表明，PSO算法具有简单易实现、全局搜索能力强、计算效率高和适合并行处理等特性，适用于多种优化问题的求解。因此，PSO算法在实际应用中具有广泛的潜力和价值。未来，可以进一步探索PSO算法在更复杂、更实际的优化问题中的应用，并对其进行改进和优化，以提高其性能和实用性